畢氏定理、三視圖、對稱、相似形、三角形的性質、多面體、內心⋯⋯我們與這些數學名詞的距離,難道只在國中的時候相交,然後就都是空集合嗎?
讓我們一起成為幾何控的摺紙咖吧!泛科學本月選書攜手臉譜出版社,透過李政憲老師生動的說明,從日常生活中常見的影印紙談起,帶著大家一起完成《藝數摺學》書中的作品,探討其中的數學概念。
直接運用隨手可得的色紙、影印紙或撲克牌,或搭配使用隨書附贈模板,按照書中步驟或及線上示範影片完成,動動手更能幫助你了解蘊含其中的數學幾何概念!
*敬請期待泛科好書搶先看:
https://pansci.asia/archives/category/文章類型/好書搶先看
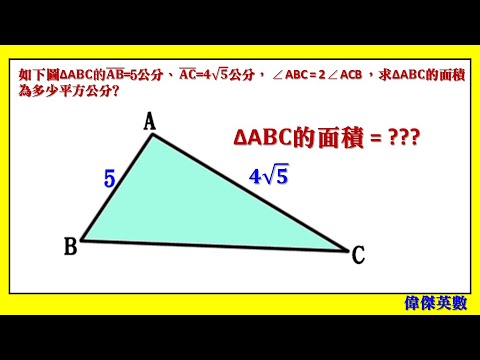
同時也有3部Youtube影片,追蹤數超過11萬的網紅GreatKidsLearning,也在其Youtube影片中提到,利用等腰三角形性質、畢氏定理、三角形面積公式來解題 歡迎大家加入會員,贊助此影音頻道...
國中幾何性質 在 Dung Kai-cheung 董啟章 Facebook 的最讚貼文
明周專欄:我死,故我在
說起笛卡兒,人人都知道他的名言:「我思,故我在。」此語第一次出現在他以法文寫成的《談談方法》(Discours de la Méthode)(1637),原文為”je pense, donc je suis”。後來在《哲學原理》(Prinicipia Philosphiæ)(1644)中再以拉丁文表述為”ego cogito, ergo sum”,簡稱為”cogito, ergo sum”,英文譯作”I think, therefore I am”。這個句式往後成為了哲學史上最常被惡搞的對象。「我X,故我在」的玩笑層出不窮,大家不妨自行創作。
至於真的讀過笛卡兒的人,可能不多。甚至把他批判得體無完膚的人,也很可能沒有細心讀過他的著作,最多是翻翻《談談方法》和《第一哲學沉思集》(Meditationes de Prima Philosophia)。大家感興趣,又或者是集中攻擊的,是他的形而上學。但是,笛卡兒從一開始,研究重點其實在自然哲學或物理學(即後來廣義的科學),而他到了命終之時,最重視的也是自己在這方面的成果。
笛卡兒在一五九六年生於法國中產家庭,家族多從事法律職務,可以說是國王的法務執行官。此類職位可以用錢購買,之後收入終身無憂,屬於「第三等級」中之高層。(法國舊王朝社會分為三個等級:第一等級為貴族,第二等級為神職人員,餘為第三等級。)笛卡兒大學畢業後,也曾多次考慮走這條路。在猶豫不決之際,他決定離開法國,見識這個世界。他加入過軍隊,當過紳士士兵,但似乎未曾參與實戰,只是乘機四處遊歷,有點像今天的工作假期。期間結交了一些學者,開始研究數學,以至光學等。
他一六二九年移居聯合省份(即以荷蘭為首的七省聯合共和國),一住便是二十年。他的所有哲學和科學成果,也是在這二十年間產生。他有一個奇怪的習慣,就是不停更換居住地。在荷蘭便住過七、八個城鎮,地址也很不確定。他的理由是逃避社交的打擾,專心從事研究工作。但他同時維持着一個有效的通訊網絡,讓他跟當代學界保持聯繫,獲知最新動向。他的一個主要通信人,是巴黎的梅森神父(Marin Mersenne)。此人亦是博學家,交遊廣闊,有「歐洲郵箱」的稱號。笛卡兒給人一個避世的隱居者的形象,連對梅森也不告知對方自己的地址,信件往往要經過多番的轉遞。
從一六二九年至一六三三年,笛卡兒潛心寫作一部自然哲學巨著,名叫《世界》(Le Monde)。《世界》的第一部分為〈論光〉,是通過對光的性質的探討,去推出他的物理學,即物質的構成、物理運作的規律,以至整個宇宙的生成過程。那是極具野心的一部著作,提出的是嶄新的宇宙機械論。此書第二部為〈論人〉,以第一部分的理論為基礎,提出了人體機械論,以及靈魂和身體的二元論。後者所說的是,人的生理部分是機械性的,跟動物或自動人偶(automaton)沒有分別,但人具有理性,而此理性即人的靈魂。所以,「人」的定義是機械肉體和理性靈魂的結合。笛卡兒認為,兩者的接合點在腦部的松果體。
一六三三年中從羅馬傳來了壞消息。伽利略的《關於兩大世界體系的對話》(即教會認可的托勒密地心說和哥白尼的日心說)被宗教裁判所查禁,伽利略被控以「違反教義和道德」及「高度懷疑為異端」被囚禁。笛卡兒立即終止了《世界》的寫作,甚至一度考慮把手稿燒毀,後來決定把它藏起來。往後無論朋友如何勸誘他,他也拒絕把它公開。他不願意成為真理的殉道者。但是,他還是忍不住把當中的一些不觸及教義的部分,以分拆形式發表。他的第一部出版的著作《談談方法》,主角其實是當中的〈屈光學〉、〈流星〉和〈幾何學〉三篇科學論文,而行文鬆散的〈談談方法〉只是前言。但是,後世幾乎都把三篇論文刪除,把序言當作獨立著作出版。
笛卡兒明知自己的物理學是不容於教義的,所以他千方百計去說服教會,自己是一個虔誠的教徒。最直接的方法,就是搞起形而上學來。於是便出現了一個科學家不應該染指的神學辯解《第一哲學沉思集》。他試圖以理性證明靈魂的存在和不滅(「我思故我在」,所以靈魂可以獨立於身體感官),以及神的存在。很可惜他在一開始便採用了懷疑論的方法,然後才一一把懷疑破除。這令一些批評者認為,他反而給予懷疑論者太強的火力,削弱了讀者對信仰的信心。他的論敵甚至認為,他根本就是個偽裝的無神論者。
可以說,笛卡兒在世時既嘗試討好教會,但又希望以偷龍轉鳳的方法,以他的一套新式學說取代過時的經院哲學。這做法並沒有取得成功,反而惹來了一次又一次的爭議,令他為自辯而疲於奔命。而他最在意的科學研究,卻沒有完整發表的機會,已發表的也沒有得到很高的評價。到了他生命的後期,一直驕傲自信的他的確變得有點心灰意冷。可能是因為這樣,他在瑞典女皇克里斯蒂娜的多番邀請下,終於答允了那趟「致命」的旅程。
一六四九年九月,笛卡兒從阿姆斯特丹上船,前往斯德哥爾摩。能成為一個女皇的私人哲學導師,無異於找到一個強大的贊助者,是以後發表著作的堅固後盾。但是,在出發前笛卡兒已有不好的預兆。他把重要的書信和手稿託付友人,並交代了自己的後事。克里斯蒂娜把哲學課的時間定在清晨五點,這對於懼怕北國嚴冬的笛卡兒來說是極大的折磨。一六五零年二月十一日,笛卡兒在瑞典因肺炎病逝。
《世界》於笛卡兒死後由追隨者整理,於一六六四年出版。隨後便開始了崇尚理性的啟蒙時代
國中幾何性質 在 李傑老師 Facebook 的最讚貼文
9年級會考生看過來!!!
台大補習班 數學名師群
精心整理的數學重點 超有用
仔細研讀 必考高分
Go go go go go go ……
來來來,筆記本準備好,
數學科致勝關鍵一次掌握!!
有看沒有懂的部分,
趕快利用時間釐清清楚~~
數學科會考30天衝刺重點
針對國中會考數學科考前準備:
會考難度為難易適中,較刁鑽的題目並不會出現太多,建議先把基本觀念及基本題型做熟,再來鑽研進階的題型。
會考考試時間80分鐘,總題數約25-30題,所以同學平時練習就必須習慣限時練習,才能適應考試時的做答速度。
考試的叮嚀:
考試難度難易適中,而且考題順序有先易後難的趨勢,所以前面做答不要花過多的時間,以免後面考題無法完成做答,再來非選部份盡量不要繳白卷,非選採取部份給分,重點在於解題的策略與表達,表達出解題策略越完整分數越高,所以非選記得務必盡量做答。
1.正負數與數線:
(1)「絕對值」代表「到原點的距離」、「相減取絕對值」
代表「兩點距離」
(2)科學記號的應用問題通常都會搭配四則運算
(3)新舊數線轉換切記「差成比例」
2.因倍數與公因倍數:
質數的判定、互質的判定還有短除法請熟練!
3.分數:
(1)四則運算切記「先乘除,後加減,但次方優先!」
(2)括號的處理務必「由小到大」且小心變號!
4.一元一次方程式:
應用題考列式
5.二元一次方程式:
(1)加減消去法
(2)代入消去法
(3)應用題
6.坐標平面:
(1)基本的象限考正負;點的移動x右加左減,y上加下減
(2)水平線y相同,鉛直線x相同
(3)二元一次直線方程式畫圖!
7.比與比例:
雙比例問題,務必調整到符合題意
8.函數:
線型函數應用問題可以利用「差成比例」處理!
9.一元一次不等式:
(1)基本的一元一次不等式求x範圍
(2)乘除負數須變向
10.乘法公式與多項式:
(1)乘法公式求值請觀察數字之間的關聯性
(2)多項式長除法
(3)因式倍式關係。
11.二次方根與勾股定理:
(1)基本的化成最簡根式、有理化、四則運算
(2)根號估計
(3)勾股定理搭配幾何一起考
12.因式分解:
(1)提公因式
(2)十字交乘
13.一元二次方程式:
(1)因式分解求x
(2)配方求x
14.等差數列:
(1)基本的循環用除法看餘數
(2)等差數列換首項公差處理
(3)等差數列求和
15.平面幾何:
(1)對稱圖形
(2)外角定理
(3)中垂線性質到兩端點等距、角平分線性質到兩夾邊等距
(4)30度-60度-90度 邊長比「1:根號3:2」
16.三角形:
(1)三角形兩邊之和大於第三邊
(2)大角對大邊小角對小邊偶爾會出
(3)三角形的全等證明
17.平行與四邊形:
(1)平行時,同位角、內錯角相等,同側內角互補
(2)遇梯形常做的幾種輔助線
18.相似形:
(1)AA相似
(2)相似形的「對應角相等」、「對應長成比例」
、「面積比等於對應長度平方比」
19.圓形:
(1)扇形、弧長、弓形
(2)相切要想到垂直與切線段等長
(3)圓周角、弦切角
20.三角形的三心:
(一)外心:(1)到三頂點等距
(2)直角三角形外心在斜邊中點
(二)內心:(1)到三邊等距
(2)r的兩種求法請複習
(三)重心:(1)中線長度比為2:1
(2)面積六等分
21.二次函數拋物線:
(1)開口的方向和大小
(2)配方法求頂點求最大最小
(3)平移要想到看頂點的移動
22.立體圖形:
(1)展開圖還原
(2)柱體的體積與表面積
23.統計:
(1)盒狀圖和圓餅圖的四分位數
(2)次數分配圖呈對稱,平均數和中位數會相等!
24.機率:
(1)列表討論
(2)畫樹狀圖
國中幾何性質 在 李祥數學,堪稱一絕 Youtube 的最佳解答
追蹤我的ig:https://www.instagram.com/garylee0617/
加入我的粉絲專頁:https://www.facebook.com/pg/garylee0617/
有問題來這裡發問:https://www.facebook.com/groups/577900652853942/
喜歡這支影片,記得按個"喜歡",並且分享
訂閱就可以看到最新的影片
你最棒,記得按鈴鐺^^
國中會考總複習:https://www.youtube.com/playlist?list=PLOAKxvSm6LGlbMqjF4W6ElHM_lrFZijkg
抖音精選:https://www.youtube.com/playlist?list=PLOAKxvSm6LGmoWuzdrsxoeKQBR_GgZyIk
學測考前猜題:
https://www.youtube.com/playlist?list=PLOAKxvSm6LGko-fghK4k3eZJ23pmWqN_k
指考數甲數乙總複習
https://www.youtube.com/playlist?list=PLOAKxvSm6LGlrdoVFRflK46Cm25CGvLBr
數學思考題型:https://www.youtube.com/playlist?list=PLOAKxvSm6LGmx__4F2KucNWpEvr1rawkw
關於數學的兩三事:https://www.youtube.com/playlist?list=PLOAKxvSm6LGlD5ABfGtLkOhNIRfWxIRc5
高中數學重要觀念解析:https://www.youtube.com/playlist?list=PLOAKxvSm6LGkzAh5k3h-CI0-clwS7xsWm
高中數學講座:https://www.youtube.com/playlist?list=PLOAKxvSm6LGmgafYQliX1Ewh2Ajun9NNn
統測考前猜題:
https://www.youtube.com/playlist?list=PLOAKxvSm6LGkP_Nvl8iToZUWNfOHT42Pg

國中幾何性質 在 李基銘漢聲廣播電台-節目主持人-影音頻道 Youtube 的最佳貼文
本集主題: #雕塑展 #黃仲傑專訪
▲探遙望的軀體 黃仲傑以雕塑呈現對結構體的想像
▲喜歡電影、動畫、漫畫等影像類的黃仲傑,也對建築結構與房屋樣式相當有
興趣,在創作中常會在結構上加入一些建築的符號,希望能夠在這些要素之中,達到空間與敘事之間的平衡。
一路從美術體系走來的藝術家黃仲傑,幼稚園時期便進入畫室學習,從小對繪畫有著相當熱忱的他,對於任何喜愛的事物都有將它臨摹下來的渴望。當時的學習環境有別於一般升學取向的畫室,少去了制式化的術科教學,一切都是以學生自己的意願為主,畫室老師本身是個創作者、也是個基督教徒,仲傑也從老師那感受到他對藝術的純粹熱誠。
此後的他開始以寫實技巧為當時的目標,不斷地在素描與水彩之間周旋,「色彩與色彩之間自然的縫合的種種經驗,深深烙印在腦海裡吸引著我。」黃仲傑這麼說著,於是在幾年的磨練之間,他逐件練就了在繪畫上的扎實底子,促使他更早地跳脫追求技巧的框架,進而從中思考創作的問題、以及藝術對他的意義。
▲藝術史的啟蒙
就讀師大附中美術班時,也邁入了黃仲傑的啟蒙期,「能K能玩」為學校的標語,一方面在課業上雖然有高標準的要求,另一方面又積極鼓勵學生加入社團,增加多元學習的機會。高三時的美術史課程尤其令他印象深刻,當老師淺略的介紹各個時期的藝術家時,黃仲傑也從這些歷史名作裡面得到一些啟發,這樣的環境也使他的眼界打了開來,誘發他閱讀許多書籍,在慌亂的價值觀拼組的過程中,找尋自己的價值與藝術的定義,最終使他確定了之後學習雕塑的道路。
在高中升大學的這個階段,也是黃仲傑從繪畫到學習雕塑的轉換期。大一時嚴密的素描課程,用以增進學生對形體的掌握能力,與泥土塑造所需要的觀察力相輔相成;在藝用解剖學的課程中,老師教導他們拼組骨骼、記錄肌肉的起始處,更藉由直接去觀看大體等方式,徹底充實了他在人體結構上的認知。
▲席勒的雕塑線條與其迷人的身體結構
在美感上,埃貢·席勒(Egon Schiele)是影響黃仲傑最深的藝術家,從他畫中對肌肉的線條勾勒,同時又精準的掌握了各大人體特徵的結構關係,還有其所安排的色彩,同時兼具圖案式的象徵性,以及區分骨骼與肉塊之間層次的功能性,著實地令他著迷。而在整個一年級中,他就在這樣人體結構的訓練與席勒繪畫的相互薰陶下度過。接著到了二年級時,黃仲傑以初學的木雕創作來投件,當大多數同學仍在處理人物或動物的形象時,他轉而去追求關於空間的題材。
▲城市漫步 靈感始於隨處可以見的建築
感受,在過去充斥著考試的升學時期,生活的步調緊湊煩悶,唯一能讓他心情安定下來的方式就是散步,利用下課之餘游走在巷弄間的小路中,觀看著台灣特有組合屋式的結構層次,又或者是觀察著各家的房屋裝潢、想像著他們的生活樣貌等等。然而,「在這樣雜亂無章、毫無美感訴求的生活型態中,我卻是看得相當出神。」,黃仲傑更表示,從街道巷弄裡的觀看當中,反而激發他找尋出這些建築中的結構與層次,希望能將他轉換成一種語彙,放入到自己的雕塑當中。
▲雕塑擁有能把握的實體魅力
「雕塑對我而言,其魅力來自於那強烈的存在感。」黃仲傑認為,雕塑擁有那可觸摸,可實在地再現、把握的性質,但與繪畫相較之下,似乎又缺少了點敘事性及自由度。後期的創作中,他融合了對人體結構的感知、以及結合建築空間元素的概念為內容,這種透過將身體部位的概念化、符號化,然後再放於一個結構之中,或是將一結構造型置於人體之中的形式,成為他日後主要的創作基礎。
過去在關於人體的創作上,黃仲傑傾向於凸顯結構性的造型和線條,試圖在人體上呈現像似建築體般垂直聳立、幾何化的沉靜意象,這樣的表現我們也可以觀察到,似乎是來自於他內心中對於結構與秩序的渴求。因此在造型上,他對於曲線、及任何具有韻律的線條都會相對地被排除,最終使得整體呈現出冰冷、無生氣的調性。
自己意識到身體作為載體的軀殼意象,就像是建築體一般客觀的場域,提供著思緒與情感運作的冰冷空間,「或許就像廢墟一樣,只能透過柱子、牆面、地板等使用的痕跡,去感受其過往人的存在。」對於這樣身體上、肉體上的想像,
黃仲傑也不斷地思索著,如何透過造型上的安排,來喚起那樣的感知狀態。
▲黃仲傑–以軀殼做為結構的載體,融合為人體和空間的無限想像。
黃仲傑簡歷:1993.1.11出生
學歷:
2005 畢業於博愛國小
2008 畢業於五常國中美術班
2011 畢業於師大附中美術班
2011 就讀於台灣藝術大學雕塑系
2015 就讀台北藝術大學美術創作研究所
展歷:
2011 台灣藝術大學雕塑系第二屆袖珍雕塑 佳作
2012 台灣藝術大學雕塑系第三屆袖珍雕塑 入選
2013 國立台灣藝術大學102學年度師生美展 佳作
2014 台灣藝術大學雕塑系第五屆袖珍雕塑展 入選
2014 台灣藝術大學雕塑系第五屆袖珍雕塑展 入選
策展單位粉絲頁: 金車文藝中心(承德館)
展出日期:2017/01/14-2017/03/05
開放時間:每日11:00-18:00(周一休館)
金車承德館地址:台北市承德路三段131號4樓